37. Почта спонсора
Все вы помните задачу “Слово спонсора” с новогодних соревнований. Напомню кратко проблему,
стоявшую в этой задаче: после завершения соревнований спонсор пожелал разослать
победителям призы.
Но почтовая система не совершенна и не всем участникам
призы могли быть доставлены. Конкретнее, в стране есть n почтовых отделений,
пронумерованных от 1 до n.
Спонсор отправляет призы с отделения под номером s. Также нам известны пары отделений, имеющих связь между собой, то
есть, между какими отделениями может передаваться почта.
Перед новыми соревнованиями спонсор решил наперед
перестраховаться и гарантировать возможность доставки призов. Для этого спонсор
готов за свои средства установить несколько новых связей между некоторыми
парами почтовых отделений. Ваша задача – посчитать, какое наименьшее количество
новых связей должен создать спонсор, чтобы призы можно было доставить после
соревнований всем участникам, несмотря на то, где они проживают и каким
почтовым отделением пользуются.
Вход. В первой строке заданы три числа – количество отделений n (1
≤ n ≤ 105), номер отделения, которым пользуется спонсор s (1 ≤ s ≤ n) и количество существующих связей между парами отделений k (0 ≤ k ≤ 105).
В следующих k строках
записано по 2 числа a и
b – номера отделений, между
которыми осуществляется перевозка почты (a
и b – разные числа с интервала
[1; n]). Все пары (a, b)
различны.
Выход. Выведите наименьшее возможное количество новых
связей, которые необходимо создать, чтобы почту можно было доставить с
отделения s в любое другое отделение.
|
Пример входа |
Пример выхода |
|
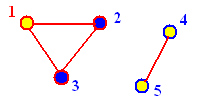
5 1 4 1 2 2 3 1 3 4 5 |
1 |
РЕШЕНИЕ
система непересекающихся
множеств
Анализ алгоритма
Количество
новых связей равно числу компонент связности графа минус 1. Поскольку n ≤ 105, то для решения задачи
будем использовать систему непересекающихся множеств с эвристиками.
Реализация алгоритма
Объявим
рабочие массивы.
vector<int> parent, depth;
Функция Repr ищет представителя множества, которому принадлежит
вершина v.
int Repr(int v)
{
if (v == parent[v]) return v;
return parent[v] = Repr(parent[v]);
}
Функция Union объединяет множества, которым принадлежат вершины x и y.
Множество с меньшей высотой присоединяется к множеству с большей высотой.
void Union(int x, int y)
{
x = Repr(x), y = Repr(y);
if (x == y) return;
if (depth[x] < depth[y]) swap(x, y);
parent[y] = x;
if (depth[x] == depth[y]) depth[x]++;
}
Основная часть программы. Читаем входные данные.
Инициализируем массивы.
scanf("%d %d %d", &n, &s, &k);
parent.resize(n
+ 1);
depth.resize(n
+ 1);
for (i = 0; i <= n; i++)
parent[i] = i;
Читаем ребра графа. Производим операцию Union над парой вершин каждого ребра.
for (i = 0; i < k; i++)
{
scanf("%d %d", &a, &b);
Union(a, b);
}
Количество полученных множеств равно числу компонент
связности графа.
for (c = 0, i = 1; i <= n;
i++)
if (parent[i] == i) c++;
Выводим число новых связей, которое следует построить.
printf("%d\n", c - 1);
Реализация алгоритма – классы
#include <cstdio>
#include <algorithm>
#include <vector>
using namespace std;
int i, n, s, k, a, b;
class dsu
{
public:
vector<int> parent, depth;
dsu(int n)
{
parent.resize(n + 1);
depth.resize(n + 1);
for (int i = 0; i <= n; i++)
parent[i] = i;
}
int Repr(int v)
{
if (v == parent[v]) return v;
return parent[v] = Repr(parent[v]);
}
void Union(int x, int y)
{
x = Repr(x), y = Repr(y);
if (x == y) return;
if (depth[x] < depth[y]) swap(x, y);
parent[y] = x;
if (depth[x] == depth[y]) depth[x]++;
}
int getSets()
{
int cnt = 0;
for (int i = 1; i <= n; i++)
if (parent[i] == i) cnt++;
return cnt;
}
};
int main(void)
{
scanf("%d %d %d", &n, &s, &k);
dsu ds(n);
for (i = 0; i < k; i++)
{
scanf("%d %d", &a, &b);
ds.Union(a, b);
}
printf("%d\n", ds.getSets()
- 1);
return 0;
}
Java реализация
import java.util.*;
public class Main
{
static int parent[], depth[];
static int Repr(int v)
{
if (v == parent[v]) return v;
return parent[v] = Repr(parent[v]);
}
static void
Union(int x, int y)
{
x = Repr(x); y = Repr(y);
if (x == y) return;
if (depth[x] < depth[y])
{
int temp = x; x = y; y = temp;
}
parent[y] = x;
if (depth[x] == depth[y]) depth[x]++;
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
int s = con.nextInt();
int k = con.nextInt();
parent = new int[n+1];
depth = new int[n+1];
for(int i = 0; i <= n; i++) parent[i] = i;
for(int i = 0; i < k; i++)
{
int a = con.nextInt();
int b = con.nextInt();
Union(a,b);
}
int c = 0;
for(int i = 1; i <= n; i++)
if(parent[i] == i) c++;
System.out.println(c - 1);
con.close();
}
}
Java реализация – классы
import java.util.*;
class dsu
{
int parent[], depth[];
public dsu(int n)
{
parent = new int[n + 1];
depth = new int[n + 1];
for (int i = 0; i <= n; i++)
parent[i] = i;
}
public int Repr(int v)
{
if (v == parent[v]) return v;
return parent[v] = Repr(parent[v]);
}
public void
Union(int x, int y)
{
x = Repr(x); y = Repr(y);
if (x == y) return;
if (depth[x] < depth[y])
{
int temp = x; x = y; y = temp;
}
parent[y] = x;
if (depth[x] == depth[y]) depth[x]++;
}
public int getSets()
{
int cnt = 0;
for (int i = 1; i < parent.length; i++)
if (parent[i] == i) cnt++;
return cnt;
}
}
public class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
int s = con.nextInt();
int k = con.nextInt();
dsu ds = new dsu(n);
for(int i = 0; i < k; i++)
{
int a = con.nextInt();
int b = con.nextInt();
ds.Union(a,b);
}
System.out.println(ds.getSets() - 1);
con.close();
}
}